こらぼジャーナル（10）まみの丸　〜一緒におもしろがる〜

前回のこらぼジャーナルno’9で紹介した、「探究の算数」で行った「1枚の紙から箱の形を作る」の全体レクチャーのあと、ほとんどの子どもたちは、自分の探究課題に戻っていったり、この時に学んだことを生かして、「街並みを紙の立体で作る」という協同探究へと向かっていったりしました。

街並みを紙の立体で作る協同プロジェクト

でも、こうのすけと同じように、別のインスピレーションを受けて、自分なりの探究の入口を見つけた子がいます。

まみは「探究の算数」に参加する2年生の女の子です。複合立体の展開図まで取り組んだ後、その日はこうのすけのサイコロ作りに刺激されてか、まみもサイコロ作りにはまります。大きさの違うサイコロを3つ作りました。次週の「探究の算数」の日、まみは何気なく「丸の立体って作れるのかな」と疑問を口にしました。（丸？うーん、球のことかな？）と思い詳しく聞いてみると、どうやらそのようでした。おー、おもしろいところに興味をもったなぁと感心しながら、「作ってみる？」と投げかけると、「やってみる！」と元気な返事が返ってきました。

さてしかし、いきなり「じゃあやってごらん」と言えるほどこの探究テーマは簡単ではありません。ようやく立方体の作り方がわかった子にとって、球を作るというのは、とっかかりに何をすればいいのか皆目見当もつかないでしょう。ですので、私のほうから、球の展開図をネットで調べてみようと提案します。一緒にパソコンの画面をのぞいてみると…出るわ出るわ、山ほどの展開図が出てきます。球の展開図の無料作成サイトまであるんですね。めっちゃ難しそうな展開図に、まみは色を失いそうになりますが、いくつか簡単そうなものもあります。そして、私のほうには最初からちょっとした目論見がありました。前に作った立方体、これ実は正六面体です。ですから、正多面体を面の少ない順に作っていけば、だんだんと見た目は球に近づいていくんじゃないだろうかと考えたのです。その途中でいろいろと気づくことがあれば、それが学びになるのではないかと…。

ということで、まずは正十二面体（正八面体はあまり丸っぽくないのでとばしました）にチャレンジ。それと、ネットの中で見つけた球に近づくもうひとつの展開図のタイプ、紡錘形（まみはこれをしずくの形と呼んでいました）の面をつなげていくというもの、これにもチャレンジしたいというので用紙を用意しました。さっそくちょきちょきはさみで切って作り始めます。こうのすけも興味をもって手伝いにきます。

　　　しずく形（紡錘形）を6枚をつないだ立体　　　　　　　　　　　　　正十二面体

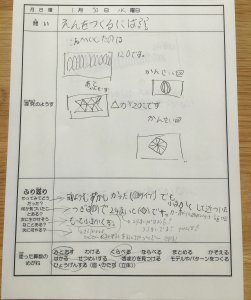
できあがった2つの立体が上のものです。立方体と比べるとすでにもう丸（球）に近づいているのがわかります。それはまみの探究ノートにもしっかりと書かれています。

（画像をクリックすると拡大します）

探究のようすのところには、「この形（しずくの形）で丸をつくる。これをこまかくするともっと丸になる。ほかには（正十二面体）これももっと小さくするとやはり丸にちかづく」と書いてあり、ふり返りのところには、「小さくすると丸にちかづく」「どんどん小さくして丸に近づけさせる」と書いてあります。まみはしっかりと気づいています。

次週のプロジェクトの日、さらに小さくしたものにチャレンジします。しずくの形は12枚になり、正多面体は正二十面体です。当然作業も難しくなり、細かな技術が必要になります。でも、まみはとても器用で丁寧です。難しい2つの立体を完成させました。

つながる前のしずく形12枚の展開図

左が正二十面体

この日のまみの探究ノートから。

（画像をクリックすると拡大します）

「こんかいしたのは、12しずくです。あと、△が20こです。前よりむずかしかった。（しずくタイプ）でも、こまかくして近づいた。つぎはしずくで24まいと、◇でサッカーボール24めんたい？をやる。」

正多面体は正二十面体でおしまいです。ですので、2人でネットでまたいいのがないかとあれこれ探し、サッカーボールに注目します。まみは「24めんたい」（◯面体という言葉を私とのやり取りの中で覚えたと思われます）と書いていますが、サッカーボールは三十二面体です。「切頂二十面体」と呼ばれ、正二十面体の頂点を切り落としたもので、切り落とした面は正五角形になります。さあ、この切り落とすことで丸に近づいたということに、まみは気づくのでしょうか。しずく型はさらに細かくなって、24枚になります。ちょっと心配…。

さて、次週のプロジェクトの日、私もわくわくしながら展開図をネットからダウンロードして印刷しておきました。まずはしずく型から取り組みます。しかし…これは…難しい…。これ、物理的に無理でした。私も一緒にやってみたんですが、しずくとしずくの接点部分が長くなり過ぎてしまうんですね。途中までで2人して切るのを断念しました。そこまでのところで立体にしてみても、円柱にとんがり帽子が上下にくっついたような形になって、どうみても丸にはならないんです。紙とはさみと人間の技術の限界でした。

気を取り直してサッカーボールに取りかかります。面の数は多くなりましたが、順調にちょきちょき進みます。

こんな具合に彼女の探究は進んでいきました。ふだん、子どもたちの探究には、教材の準備や次の課題の設定などの介入はほとんど行わないのですが、まみのこのテーマは私も一緒に探究しました。私自身、あまり知らない領域だったからです。「丸の立体って作れるのかな？」という彼女の最初の疑問は、実は私もとても興味深く感じていたのです。ネットで調べていくうちに、「なるほど…」とか「なんと！」とか、そんなことといっぱい出会うことができました。まみもたぶんそうだったんじゃないかなと思います。理解の程度は違いますが、同じテーマを通して、同じ「感じ」を共有することは探究者の伴走者として大切にしていきたいところだと思います。「一緒におもしろがる」って大事！！一緒におもしろがるには、同じところから同じものを見ないとダメなんだと思います。探究者がおもしろがっていることを、伴走者が外から見て「おもしろそうだね〜」って共感することはできるけど、探究のプロセスを共有体験して「おもしろいね〜」って共感するのとは100万倍くらいの差があると思います。前者は見た目の「感情」を共有できるけど、後者は湧いてくる「感情」と「感覚」を共有できます。これらを共有できると、次の探究のステージが見えてきます。

（画像をクリックすると拡大します）

この日の探究ノートから。「しずくの形はいちおう丸だがあまり丸に近づかない」とのこと。まあ、本当はそうではないんですが、体験の中で気づいたことなので、そのままにしておきます。いつかまた、このことについて考える機会が必ずあります。その時に、この体験がきっと生かされるはず。その時まで待っていましょう。だってほら、この探究ノートのふり返りのところ、まみはこう書いていますよ。

「だい3きへ」¹

って。

彼女の探究は、まだまだ続いていくことでしょう。そして、私もまた、その探究に伴走して一緒におもしろがりたいと思います。

まみの作った「丸」

¹「だい3き」とは「第3期」のこと。風越こらぼは2018年度は第1期、第2期で終了しました。2019年度、第3期は6月からスタートしています。

#2019 #探究の学び